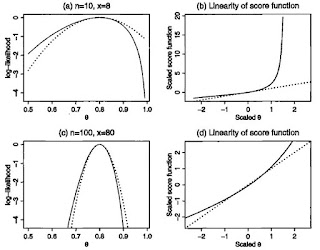
標準差與 Wald 統計量

可能性或信賴區間對 MLE 是有用的添補,認可了在一個參數 theta 的不確定性; 它比 likelihood function 更簡單。前面我們也提過 observed Fisher Information : I(theta) 也是 MLE 的添補。那麼它與基於可能性的區間的關係為何呢? 在 regular 的情形下,log-likelihood 的二次趨近運作良好, I(theta) 是有其意義的。這時我們有: Log(L(theta)/L(theta-hat)) ~ -1/2*I(theta-hat)(theta-theta-hat)^2 如此,可能性區間 { theta | L(theta)/L(theta-hat) > c } 就可趨近於: theta-hat ± - (-2*log(c))^(1/2)(I(theta-hat))^(-1/2) 在 normal mean 模型,就有一個確切的有信心水準的信賴區間 Prob(chi-squared < -2log(c)) 例如: theta-hat ± - 1.96 * I(theta-hat)^(1/2) 是一個確切的有 95% 信心水準的信賴區間。 在非 normal 的情況下,如上篇提到的有一 95%信心水準的信賴區間。注意: 設置此區間涉及兩層的趨近: log-likelihood 的二次趨近(I(theta-hat)與信心水準(Willk's) 的趨近。 也可與 normal mean 模型類比,一般 (I(theta-hat))^(-1/2) 提供了 theta-hat 的標準差訊息。常例以 'MLE{標準差}'一對的形式來報告。它主要用途是用 Wald 統計量來檢定 H0: theta = theta0。 z = (theta-hat - theta0)/se(theta-hat) 或去計算 Wald 信賴區間。例如 Wald 對 theta 95% 信心水準的信賴區間就是: theta-hat ± 1.96*se(theta-hat) 在 normal mean 模型,在 H0 條件下,這個 Wald z 統計量...