MLE 附近的性質
在 normal distribution 成立的性質，在一般情況下也會趨近成立。在所有 likelihood的應用中，我們這裡有一個實用的規則：一個合理常見的 likelihood 意味著 theta-hat 是趨近於 normal 。對 normal 模型是真的陳述，對 theta-hat 通常也會趨近於真。
我們在 "theta-hat" 附近，進行泰勒展開式，
log(L(theta)) ~ log(L(theta-hat)) + S(theta-hat)(theta - theta-hat) - 1/2*I(theta-hat)(theta - theta-hat)^2
因為 S(theta-hat) = 0 ，[我們定義 S(theta) 為 Log-likelihood function => log( L(theta)) 的第一階微分，而 theta-hat 為 MLE 使得 S(theta-hat) = 0]
log(L(theta)/L(theta-hat)) ~ -1/2*I(theta-hat)*(theta -theta-hat)^2
對上式進行一階微分 [theta 在 theta-hat 附近]，則
S(theta) ~ - I(theta-hat)*(theta - theta-hat)
上式兩邊可以一起除 - I^(1/2) ，
S(theta) /-I(theta-hat)^(1/2) ~ I(theta-hat)^(1/2)(theta - theta-hat)
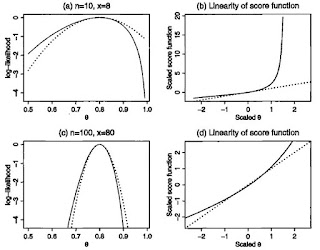
好處是去掉 scale，在檢查此泰勒二階趨近時，可以畫 出 S(theta) /-I(theta-hat)^(1/2) vs. I(theta-hat)^(1/2)(theta - theta-hat) 看是否是單位斜率(因為去掉 scale了)。
在 normal 的情況，就一定是單位斜率。 任何只要是平滑函數在就一定是 local linear，問題只於在此 local 有多寬我們可以期待看到此線性 linearity? 在理想的 normal 狀況下，I(theta-hat)^(1/2)(theta - theta-hat) 為 ~ N(0,1)，所以我們直覺上應可以至少可以檢查 -2 到 +2 之間2的情況[在圖上此範圍上進行比較]。 圖示如下:
則 log-likelihood function 的 MLE的曲率 或 standard error 將失去意義。在此情況下，有 likelihood 的集合它的 confidence interval 信賴區間，相較於曲率，對 MLE 而言是較好的補充訊息。
From: All In Likehood: Statistical modeling and Inference
留言
張貼留言