時間序列過程
A time series is a sequence of observations on a variable taken at discrete intervals in
time.1
We index the time periods as 1, 2, …, T and denote the set of observations as
( y1 y2 , , ...,yT ).
We often think of these observations as being a finite sample from a time-series stochastic process
that began infinitely far back in time and will continue into the indefinite future:
pre-sample sample post-sample
Each element of the time series is treated as a random variable with a probability distribution. As with the cross-section variables of our earlier analysis, we assume that the distributions of the individual elements of the series have parameters in common. For example, we may assume that the variance of each y_t is the same and that the covariance between each adjacent pair of elements cov ( y_t ,y_t −1 ) is the same. If the distribution of y_t is the same for all values of t, then we say that the series y is stationary, which we define more precisely below. The aim of our statistical analysis is to use the information contained in the sample to infer properties of the underlying distribution of the time-series process (such as the covariances) from the sample of available observations.
We model serially correlated time series by breaking them into two additive components:
The function g is the part of the current y_t that can be predicted based on the past. The variable ε_t, which is assumed to be white noise, is the fundamental innovation or shock to the series at time t—the part that cannot be predicted based on the past history of the series.
From above equation and the definition of white noise, we see that the best possible forecast of y_t based on all information observed through period t – 1 (which we denote It – 1) is
and the unavoidable forecast error is the innovation
Every stationary time-series process and many useful non-stationary ones can be described by equation . Thus, although most economic time series are not white noise, any series can be decomposed into predictable and unpredictable components, where the latter is the fundamental underlying white-noise process of the series. Characterizing the behavior of a particular time series means describing two things: (1) the function g that describes the part of y_t that is predictable based on past values and (2) the variance of the innovation ε_t. The most common specifications we shall use are linear stochastic processes, where the function g is linear and the number of lagged values of y and ε appearing in g is finite.
From: Fundamental Concepts of Time-Series Econometrics
Each element of the time series is treated as a random variable with a probability distribution. As with the cross-section variables of our earlier analysis, we assume that the distributions of the individual elements of the series have parameters in common. For example, we may assume that the variance of each y_t is the same and that the covariance between each adjacent pair of elements cov ( y_t ,y_t −1 ) is the same. If the distribution of y_t is the same for all values of t, then we say that the series y is stationary, which we define more precisely below. The aim of our statistical analysis is to use the information contained in the sample to infer properties of the underlying distribution of the time-series process (such as the covariances) from the sample of available observations.
We model serially correlated time series by breaking them into two additive components:
The function g is the part of the current y_t that can be predicted based on the past. The variable ε_t, which is assumed to be white noise, is the fundamental innovation or shock to the series at time t—the part that cannot be predicted based on the past history of the series.
From above equation and the definition of white noise, we see that the best possible forecast of y_t based on all information observed through period t – 1 (which we denote It – 1) is
and the unavoidable forecast error is the innovation
Every stationary time-series process and many useful non-stationary ones can be described by equation . Thus, although most economic time series are not white noise, any series can be decomposed into predictable and unpredictable components, where the latter is the fundamental underlying white-noise process of the series. Characterizing the behavior of a particular time series means describing two things: (1) the function g that describes the part of y_t that is predictable based on past values and (2) the variance of the innovation ε_t. The most common specifications we shall use are linear stochastic processes, where the function g is linear and the number of lagged values of y and ε appearing in g is finite.
From: Fundamental Concepts of Time-Series Econometrics

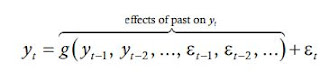


留言
張貼留言